■フィボナッチ数列と1級建築士試験問題
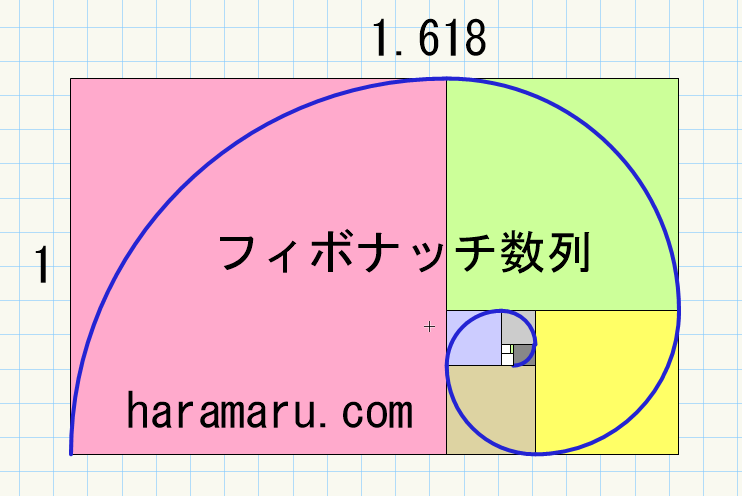
フィボナッチ数列は直前2項の和を次の項とする数列であり,並び合う2項の比が急速に黄金比に収束するため,建築においては特殊な意味をもたされている数列です。
ィボナッチ数列とは、1、1、2、3、5、8、13、21、34、55、89、144、233・・・という数列のことです。この数字で隣合う数字の比率を計算していくと、2/1=2、3/2=1.5、5/3=1.6666、8/5=1.6、13/8=1.625、21/13=1.61538、233/144=1.618というふうに、1.618に収束していきます。
古代ギリシャ以来、1:1.618は「神の比」とまで言われた「西洋の黄金比」なのだそうです。人間にとって最も安定し、美しい比率とされていて建築や美術等で使われており、「モナリザ」や「アップルのロゴ」「ピラミッド」「ミロのビーナス」「パルテノン神殿」にも使われているといいます。自然界でも、パイナップルやひまわり、シダの葉、カタツムリ、アンモナイトなど、多数がこの比率になっているそうです。上の図形のように、黄金比を持つ長方形から正方形を抜くと、また黄金比を持つ長方形が現れます。日本では、名刺の比率です。
ところで、平成25年の1級建築士の問題に出題されました。→「直前の隣接する2項の和が次の項となるような数列(フィボナッチ数列)を順次作成していくと、その連続する2項の比率は黄金比に近づく」正解は?→ ○ 1.618に近づきます。
日本にも1:1.414という「日本の白銀比」があり、A判用紙、風呂敷、法隆寺、菱川師宣「見返り美人図」等で使われています。この、1.414については、「白銀比 1.41」で解説しています。日本人らしさが見えます。
「レオナルド・ダ・ヴィンチ の黄金比」も有名です。「ウィトルウィウス的人体図」“Vitruvian man” の中の「円の半径」と「正方形の辺の長さ」の比が黄金比であると言われています。ですが、実際に比べてみると、円の半径と正方形の辺の長さの比は,0.606 ∼ 0.609 程度の値になり,黄金比 0.618 より,かなり小さい値になるそうです。根本的には同じであるのかもしれません。
最後に、日本の天才数学者 岡 潔さん「天才を育てた女房」という映画かドラマを見た記憶があります。、みちさんという奥様との、泣けてくる暖かい物語です。花びらの数が奇数でフィボナッチであることに気づきます。外国の学者からも認められますがが、国内で理解できる学者が少なく孤立していたと思います。結局、陛下から勲章を授与されることになるのですが、そのときに「奥様に語った言葉」が何だったか?もう一度見たいと思っています。どなたか、ご存じの方いらっしゃいますか?


